There are many cultural differences around the world when it comes to schoolwork and teaching, and as for  curricula, Mexican students add a new element to their study: They learn hieroglyphics in math class.

In fact, primary school students in Mexico study a few number systems, including Roman numerals, the ancient Egyptian number system, and the Mayan system for counting. They all reveal something interesting about how we can describe numbers!

In this post:

What are number systems?

Throughout history, civilizations have created their own symbols and rules to express numbers. Number symbols are often called numerals which just means “numbers written using a specific writing system.” The numbers that are most commonly used in the U.S. are called Arabic numerals or Hindu-Arabic numerals because they came from modern-day India and Arabic-speaking communities. (Interestingly, a different set of symbols is used in much of the Arab world today!)

The Arabic numerals we use in English are part of a decimal system: We group numbers in 10s, both in how we speak and in how we write out numbers. For example, the word twenty is based on the words for two and ten, since twenty is 2 groups of 10. And when we write decimals, like 8.3, the ".3" stands for 3/10 of a whole. Even the word decimal has a word for "ten" in it—that dec- is like English decade (10 years) or Spanish diez (the number 10).

But there are other ways of representing numbers, as all Mexican students learn.

Why do Mexican students study other number systems?

Mexican students learn about ancient number systems to compare them to the Arabic (decimal) system—and to learn about advantages and disadvantages in number systems. This gives them a nuanced understanding of how number symbols can represent different values, which can really help when learning about addition, subtraction, decimals, and fractions.

Roman numerals

More than 2,000 years ago, the Romans came up with their own number system. They’re still present in many places, like in movie titles, on clock faces, in names, and even in dates. Roman numerals are written using these 7 letters:

Symbol Value
I 1
V 5
X 10
L 50
C 100
D 500
M 1000

For really big numbers like thousands and millions, the Romans used one or two straight lines above the letters.

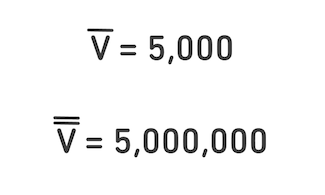
capital letter V with a single horizontal line above it is equal to 5,000. Capital letter V with two horizontal lines above it is equal to five million.

With just these 7 letters, any number can be written out, following these rules:

  • Each letter can be repeated up to three times.
  • When subtracting, a letter with a lesser value is written to the left of a letter with a greater value.
  • When adding, a letter with a lesser value is written to the right of a letter with a greater value.

Here are a few examples:

  • IV: 5 - 1 = 4 (I is written to the left of V for subtraction)
  • VI: 5 + 1 = 6 (I is written to the right of V for addition)
  • VIII: 5 + 3 = 8 (III is written to the right of V for addition, and the maximum of 3 repeated letters has been reached)
  • CCCXL: 300 + (50 - 10) = 340 (CCC is for 3 sets of 100, and X is subtracted from L to get 40)
  • MMCXII: 2000 + 100 + 10 + 2 = 2112 (the year Duolingo turns 100!)

In Mexico, Roman numerals used to be used for months when writing dates. Nowadays, months are not necessarily written with Roman numerals, but students still learn them—and they quickly realize that a lot more symbols are needed to represent numbers when using Roman numerals! But that’s not all bad: Roman numerals allow learners to practice adding and subtracting 1s, 10s, and 100s.

Egyptian numerals

The Egyptians had a number system all their own, and it had some features in common with Roman numerals, and a few important differences, too. Egyptian numerals had symbols for 1, 10, 100, 1,000, 10,000, and so on. The symbols can be repeated up to 9 times (unlike Roman numerals where the limit was 3).

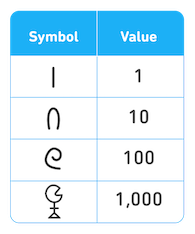
4 Egyptian symbols and their corresponding values: a straight, vertical line equals 1, a looped arch equals 10, a curved line forming a coil equals 100, and the symbol for 1,000 is a mostly complete circle (missing a "slice" so it looks like an open mouth) atop a stem and leading to a triangle base.

The symbols are based on the natural world: For example, the symbol for 100  is a coil of rope, and the symbol for 1,000 is a flower, and the little lines and triangle represent leaves (even though many students think of 1,000 as a little person!). The Egyptian numerals are fun for students to trace, and they don’t have to be written in any particular order—you simply add up the value of the symbols you see, no matter where they are!

For example, 235 can be represented as:

3 rows of Egyptian numerals, all with the same value (235). The first row is two coils, followed by 3 arches and then 5 straight lines. The second row is the 5 straight lines first, then the two coils, and finally the 3 arches. The third row is one coil, then the 3 arches, 5 straight lines, and second coil.

In the Egyptian system, the value of each number doesn't depend on its position, like in the decimal and Roman systems. Some students prefer that! But you can see that writing 9,999 using this system would make a very long number. 😅 

Mayan numerals

The Maya are a native American group from southern Mexico and Central America, and they developed their own number system as well. Mayan numerals are written from top to bottom and their value depends on their position. 

Mexican students take pride in their roots by exploring and learning this number system. However, it is quite a challenge because this is the most difficult of all three ancient number systems taught: Unlike the different decimal systems presented above, the Mayans used 20 as the base number, not 10. So instead of thinking of 62 as 6 groups of 10 (sixty) plus 2, they think of it as 3 groups of 20 plus 2.

Students in Mexico learn to write the first 3 levels of Mayan numbers. The first level contains the numbers 1 to 19. Aside from the shell-like symbol for the 0, only dots and lines are used to express the first 19 Mayan numbers:

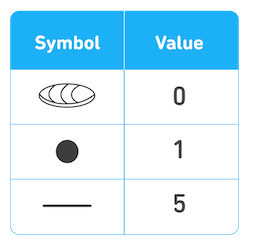
Illustration of 3 Mayan numerals and their values: a long oval that looks like a loaf of bread is for zero, a large black dot is for 1, and a flat, horizontal line is for 5.

For numbers 1-19, you can combine these numerals on top of each other, with 5s on the bottom and dots for 1s above them:

Three example equations with Mayan numerals: 3 large dots equals 3, 2 dots on top of a flat horizontal line equals 7, and 3 dots on top of two horizontal lines equals 13.

For numbers 20 or above, a dot is added above the 1s level—so any time students see dots on top of each other, they know the second level is for 20. One dot on the second level means 20, two dots means 40, etc.

Here's how 22 would be written:

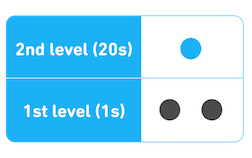
A two-level diagram: on the first level are two black dots for the ones, and above it on the second level is one blue dot representing 20.

To represent even bigger numbers in Mayan numerals, a third level is used for groups of 400 (20²). This gets complicated quickly—but it does give students a lot of practice with multiples of 20 and 400! Here's how to write 422:

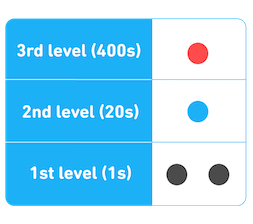
A three-level diagram: on the first level are two black dots for the ones, above it on the second level is one blue dot representing 20, and above that is a third level for the 400s with one red dot.

Mexican students use different colors for each level (like in these examples) to help distinguish 1s, 20s, and 400s, but the real Mayan system was all the same color! 

It all *adds up* to keeping your brain sharp

There's a lot to learn from other cultures and how they think about numbers, and in Mexico, students learn the advantages of having a decimal system and how easy they have it compared to Mayan students in the past! To strengthen your own decimal system skills, try out Duolingo's new math course.